الأعداد الكسرية: دليلك الشامل للفهم والتفوق
هل سبق وشعرت بالحيرة عند التعامل مع الأعداد الكسرية؟ لا تقلق! اليوم سنكتشف معاً هذا العالم الرياضي الممتع بطريقة بسيطة وواضحة. دعني أخبرك سراً: الأعداد الكسرية أسهل مما تتخيل، فقط تحتاج لفهم القواعد الأساسية وستصبح محترفاً في التعامل معها.
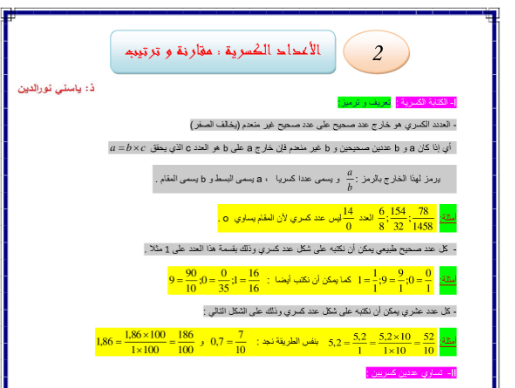
ما هو العدد الكسري ولماذا نحتاجه؟
العدد الكسري هو ببساطة عدد نكتبه على شكل خارج قسمة عددين صحيحين، أي على الشكل a/b حيث b لا يساوي الصفر.
يمكنك أن تفكر فيه كقطعة من كعكة كاملة!
- عندما تقسم بيتزا إلى 8 قطع وتأكل 3 منها، تكون قد أكلت 3/8 من البيتزا.
- وإذا أنجزت 5 واجبات من أصل 10، فأنت أتممت 5/10 من واجباتك.
- حتى نصف ساعة تكتب رياضياً على شكل 1/2 ساعة.
الأعداد الكسرية موجودة في كل مكان حولنا، نحن فقط لا ننتبه لها! الجميل في الأعداد الكسرية أنها تشمل كل الأعداد التي تعرفها. نعم، كل عدد صحيح طبيعي يمكن كتابته على شكل كسر (مثلاً العدد 5 هو 5/1).
القاعدة الذهبية في التعامل مع الكسور
هناك قاعدة سحرية يجب أن تحفظها جيداً: عندما تضرب أو تقسم البسط والمقام بنفس العدد، قيمة الكسر لا تتغير أبداً! هذه القاعدة هي مفتاح نجاحك.
تخيل أن لديك كسر 36/24، يمكنك تبسيطه بقسمة البسط والمقام على 12، فتحصل على 3/2. هذه القاعدة ستساعدك في عمليات المقارنة والجمع والطرح لاحقاً.
كيف تقارن بين الأعداد الكسرية بذكاء؟
المقارنة بين الأعداد الكسرية قد تبدو صعبة، لكن هناك طرق ذكية تجعل الأمر سهلاً:
1. الحالة الأولى: نفس المقام
كل ما عليك فعله هو مقارنة البسط فقط! مثلاً: 6/19 أكبر من 3/19 لأن 6 أكبر من 3.
2. الحالة الثانية: نفس البسط
الكسر ذو المقام الأصغر هو الأكبر! فكر معي: 5/3 أكبر من 5/8 لأن الثلث أكبر من الثمن.
3. الحالة الثالثة: مقامات مختلفة
هنا نحتاج لتوحيد المقامات أولاً، ثم نقارن البسط بعد ذلك.
استراتيجيات ذكية للمقارنة السريعة
يمكنك مقارنة الكسور مع أعداد مرجعية معروفة مثل العدد 1:
- إذا كان البسط أكبر من المقام، فالكسر حتماً أكبر من 1.
- إذا كان البسط أصغر من المقام، فالكسر أصغر من 1.
نصائح عملية لتجنب الأخطاء الشائعة
- توحيد المقامات: لا تقارن أبداً دون توحيد المقامات إذا كانت مختلفة.
- القسمة على صفر: تذكر دائماً أن المقام لا يمكن أن يساوي صفراً أبداً.
- المراجعة: راجع حساباتك بعد التوحيد للتأكد من دقة النتائج.
الأعداد الكسرية في حياتك اليومية
الأعداد الكسرية ليست مجرد أرقام على الورق، بل هي لغة عملية ستجدها في:
- تقسيم الميراث.
- حساب النسب المئوية في التجارة.
- وصفات الطبخ (مثلاً 2/3 كأس من الدقيق).
تمارين تطبيقية (هل استوعبت الدرس؟)
لنتأكد من أنك أصبحت محترفاً في الأعداد الكسرية، حاول حل هذه التمارين البسيطة قبل قراءة الحل:
التمرين 1: مقارنة الكسور
قارن بين الكسرين التاليين: 4/7 و 5/9
- الحل: لتوحيد المقامات، نضرب 7 في 9 لنحصل على 63.
- الكسر الأول يصبح: (4 × 9) / 63 = 36/63
- الكسر الثاني يصبح: (5 × 7) / 63 = 35/63
- النتيجة: بما أن 36 أكبر من 35، فإن 4/7 أكبر من 5/9.
التمرين 2: تبسيط الكسور
بسط الكسر التالي لأقصى حد: 24/36
- الحل: نبحث عن القاسم المشترك الأكبر.
- نقسم البسط والمقام على 12.
- 24 ÷ 12 = 2
- 36 ÷ 12 = 3
- النتيجة النهائية: 2/3.
التمرين 3: مسألة من الواقع
أكل أحمد 1/3 البيتزا، وأكلت ليلى 2/6 من نفس البيتزا. من أكل أكثر؟
- الحل: لنقارن الكسرين.
- نبسط كسر ليلى (2/6) بقسمة البسط والمقام على 2.
- نحصل على 1/3.
- النتيجة: أحمد وليلى أكلا نفس الكمية! (لأن 1/3 يساوي 2/6).
تذكر دائماً: كل خبير كان في يوم ما مبتدئاً. لا تستسلم، فالممارسة اليومية هي أساس التفوق. الطريق إلى النجاح يبدأ بخطوة، وأنت اليوم خطوتها بقراءة هذا المقال على نجاحي برو.